MotionWarping
MotionWarping算是一项老生常谈的动画技术了。技术本身原理并不复杂，不过UE自己却有不少的变种实现方案，对这最基础的实现思想有不断的进化和补充，目的也是为了提高算法的最终表现效果，做3A游戏真是对细节真是孜孜不倦啊。本文主要是解释MotionWarping的基础原理和UE的SkewWarping的实现原理。
DeltaCorrection和AnimationWarping
MotionWarping是动态调整动画的RootMotion使其实时对齐目标点的动画技术。
其中GDC2017有两个分享过这项技术的技术方案和应用：
Doom当时叫Delta Correction1主要是用在怪物向玩家突击，包括平面突击，跳台阶突击等
地平线则叫Animation Warping2，主要用在玩家翻越。
GDC2017两项技术的分享
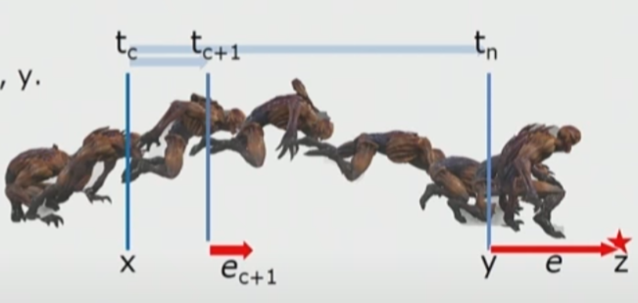
两项技术原理几乎一样，也很简单。这里以DOOM为例：
每帧计算与修正：
x是当前模型位置，$t_c$是当前当前位置动画时间
y是RootMotion动画最终位置，$t_n$是最终位置时间
z是运行时目标位置，$e$是动画最终位置y与目标位置z的差值
求得两帧缩放比$f = (t_{c+1} - t_c) / (t_n - t_c)$
下一帧应用额外变换$e_{c+1} = f * e$，使每一帧逐渐趋近z
Delta Correction图例
UE中的MotionWarping
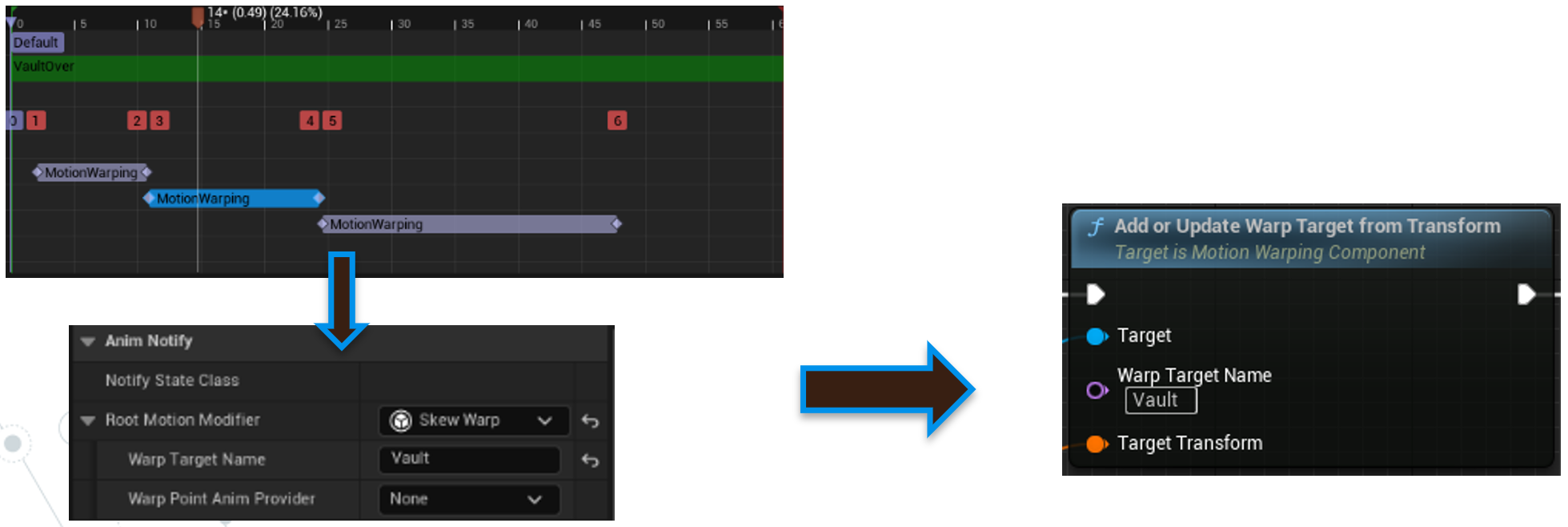
UE官方插件名为MotionWarping的插件，就包含实现上述DeltaCorrection或AnimationWarping的一个动画插件。其运作流程跟DOOM的分享一致，因而使用流程也是如此：
- 创建MotionWarping窗口，即AnimNotify开始和结束位置；
- 选择合适的Modifier；
- 设置WarpTarget的Position、Rotation。
UE使用MotionWarping的三个步骤
核心修正代码都在Modifier中
而UE提供ScaleWarp、SimpleWarp、SkewWarp、AdjustmentBlendWarp四种Modifier。ScaleWarp就是纯按比例缩放，适合Dodge之类无目标的Warping。SimpleWarp原理跟DeltaCorrection做法基本一致。
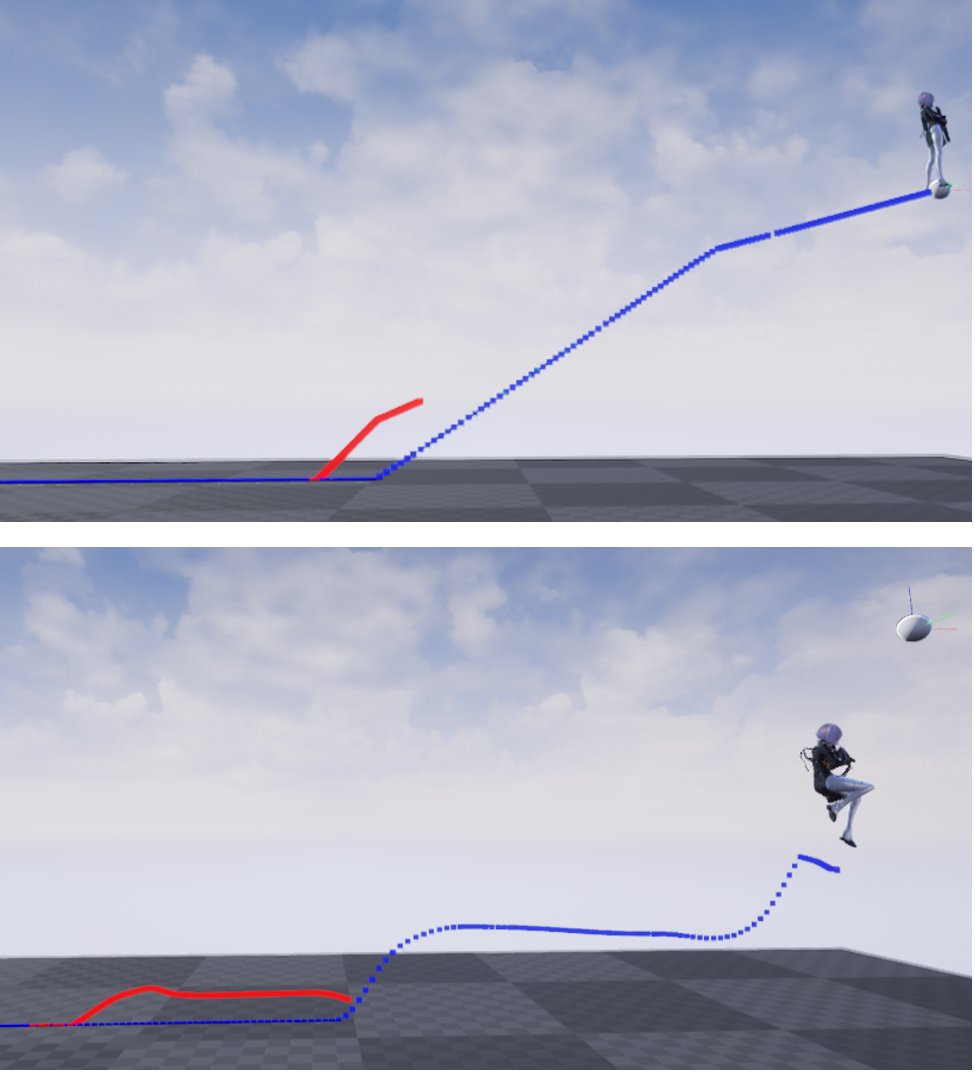
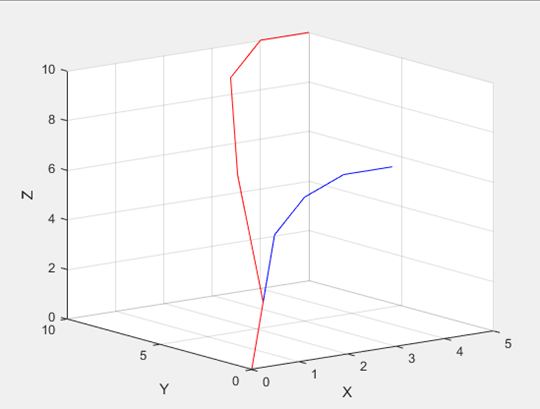
不过使用SimpleWarp也是有缺陷的：SimpleWarp本质是等比缩放。等比缩放的轨迹曲线，突变问题可能会被放大，如下图的折线。轨迹复杂的曲线，如下图由多个曲线组成的轨迹，无法到达目标点。
SimpleWarp的缺陷分别是突变问题（上图）和多峰值点无法触及目标点（下图）
SimpleWarping一般适合线性缩放，如开门动画。或者可以通过传入复杂曲线的每个最高点位置解决问题。
SkewWarp
SkewWarp是UE提供的另外一种Warping算法，中文可翻译为错切扭曲。
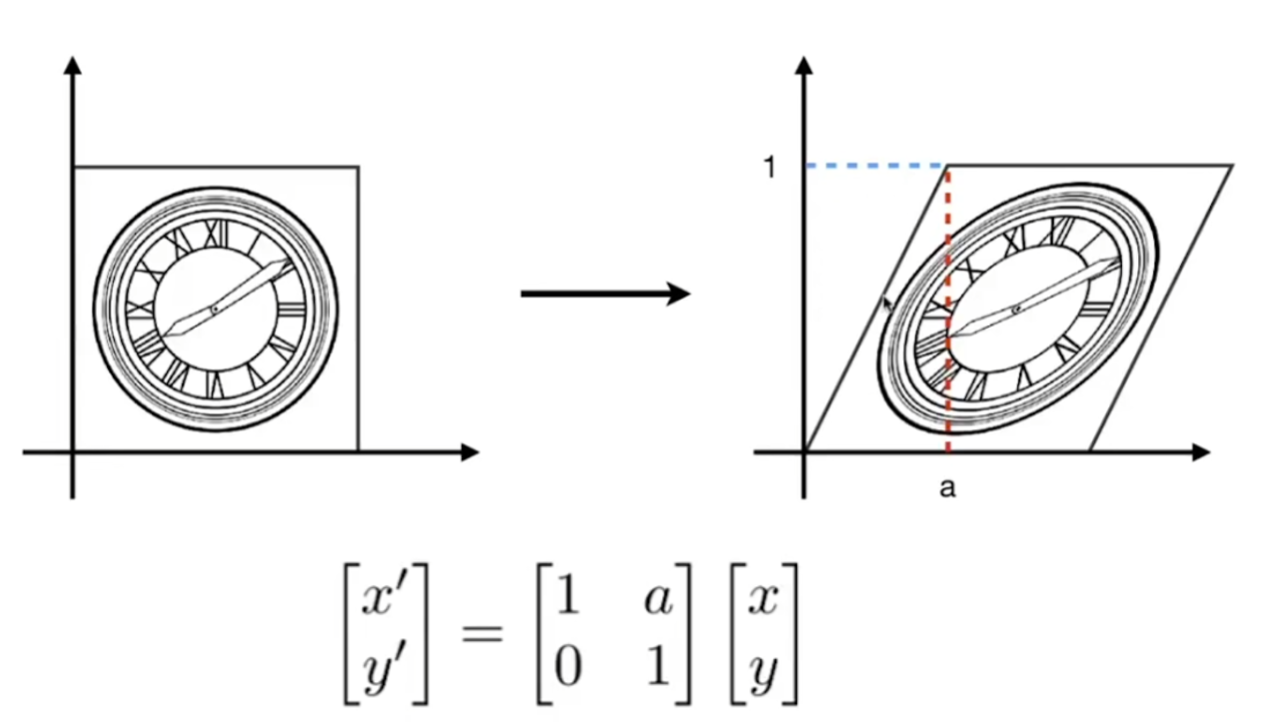
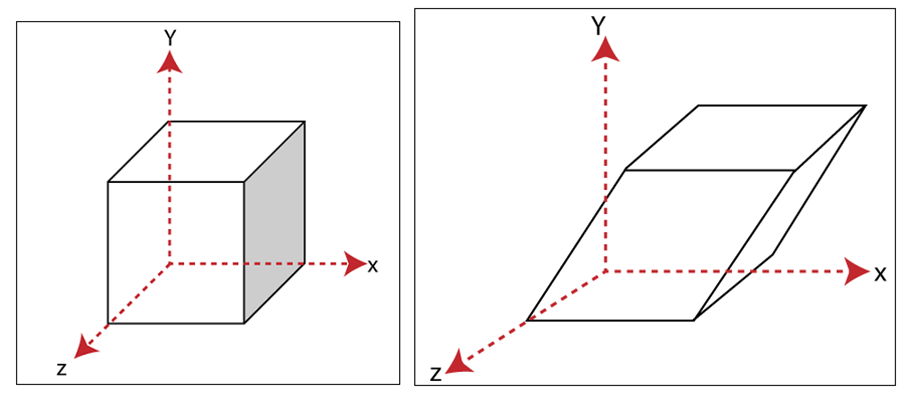
错切扭曲可缓解上述SimpleWarp的两个问题。SkewWarp的错切跟二维图像错切变换一样，通过指定某一不变轴（下图是y）进行错切，指定的轴的值则保持不变
错切的值会受到的指定的轴的值影响，如$x^, = x + ay$，$x$会受到$y$值的影响。这样又称沿着$y$轴错切。
图来自games101，二维错切的图示及其矩阵
三维错切二维的扩展：指定一个不变轴（该轴的值错切后跟原值一样），其他两轴按比例加上不变轴而得到错切值。
三维错切
三维错切可以说是在不同轴（或者说不同平面）上做二维错切。我们以x轴为例：发生错切当指定x轴不变的时候，y和z会加上x的值乘以一个常量而得。y轴和z轴同理：
三维错切三轴矩阵
回到SkewWarp，顾名思义，这算法就是通过错切的变换把RootMotion扭曲到合适的形状。
SkewWarp的目的就是构造错切矩阵。变换到以前进方向为x方向的局部坐标系，x只随着时间变化
指定x轴不变，并且只处理z的情况：
$V_e$当前位置到原动画终点的方向
$V_t$当前位置到修正目标方向
$V_c$当前位置到下一帧位置方向，将其修正到绿色虚线$V_f$
沿着x轴错切得：
$V_{fz}= V_{tz} + a* V_{tx}$
$V_{fx}= V_{tx}$
$a = tan∠(V_e,V_t)$
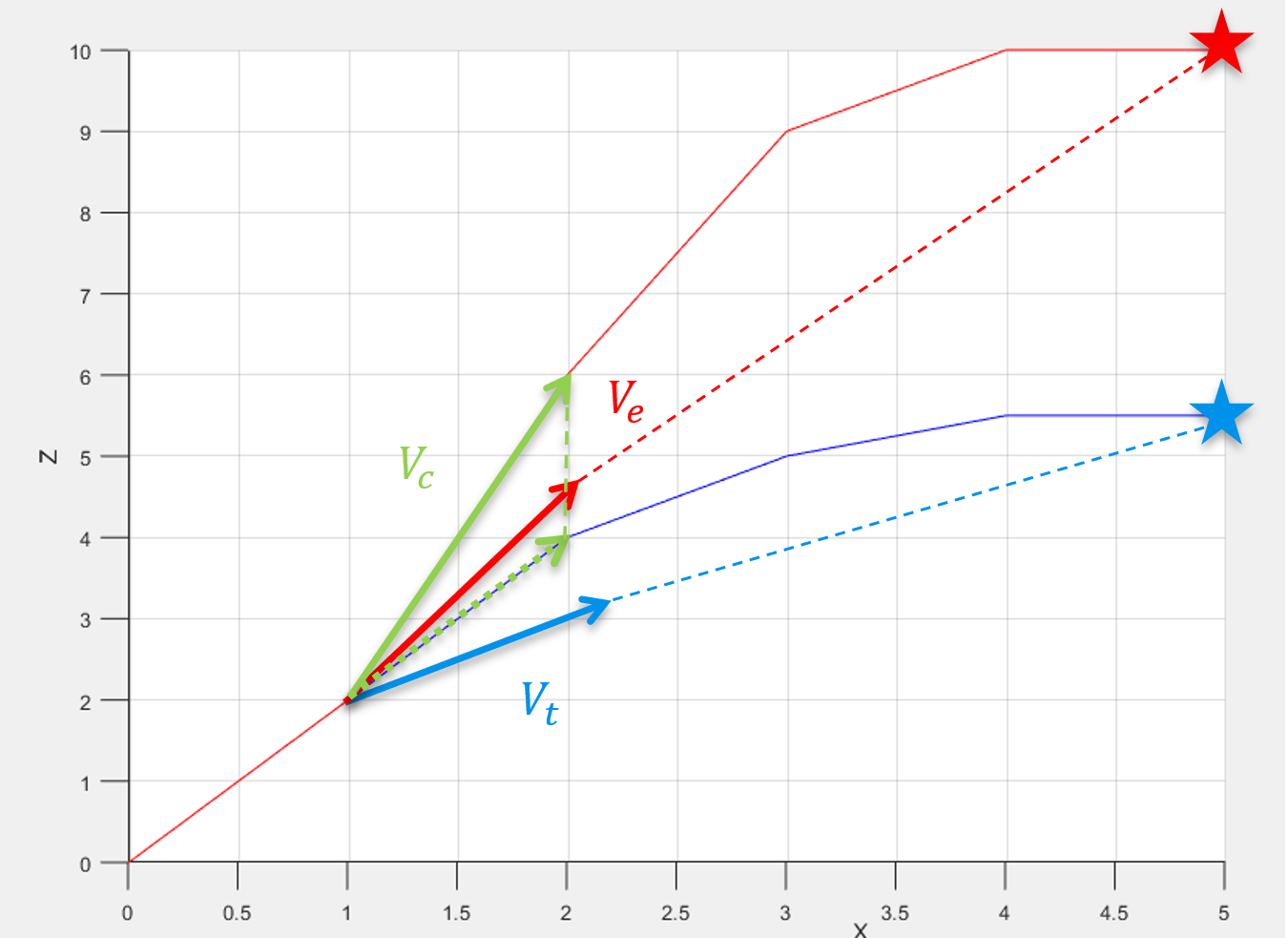SkewWarp在XZ平面的图示，蓝色为原动画轨迹，红色为修正动画轨迹，绿色为修正过程
Skew变换三维视角，XY平面也是一样的
下面公式分别是垂直XYZ平面的错切矩阵。
\[M_x= \left[ \begin{matrix} proj(𝑉_t,𝑉_e)/|𝑉_𝑒| & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \\ M_y= \left[ \begin{matrix} 1 & 0 & 0 \\ tan∠(𝑉_{𝑒𝑧},𝑉_{𝑡𝑧}) & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right] \\ M_z= \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ tan∠(𝑉_{𝑒𝑧},𝑉_{𝑡𝑧}) & 0 & 1 \\ \end{matrix} \right]\]x轴平面是前进方向，无须错切，这里以计算动画终点方向到目标方向的投影作为前进方向缩进比例。
实际计算结果是当前RootMotion的单帧Translate的T经过Warp得到:
$T^` = M_x × M_y × M _z ×T$
旋转变换跟SimpleWarp一致。
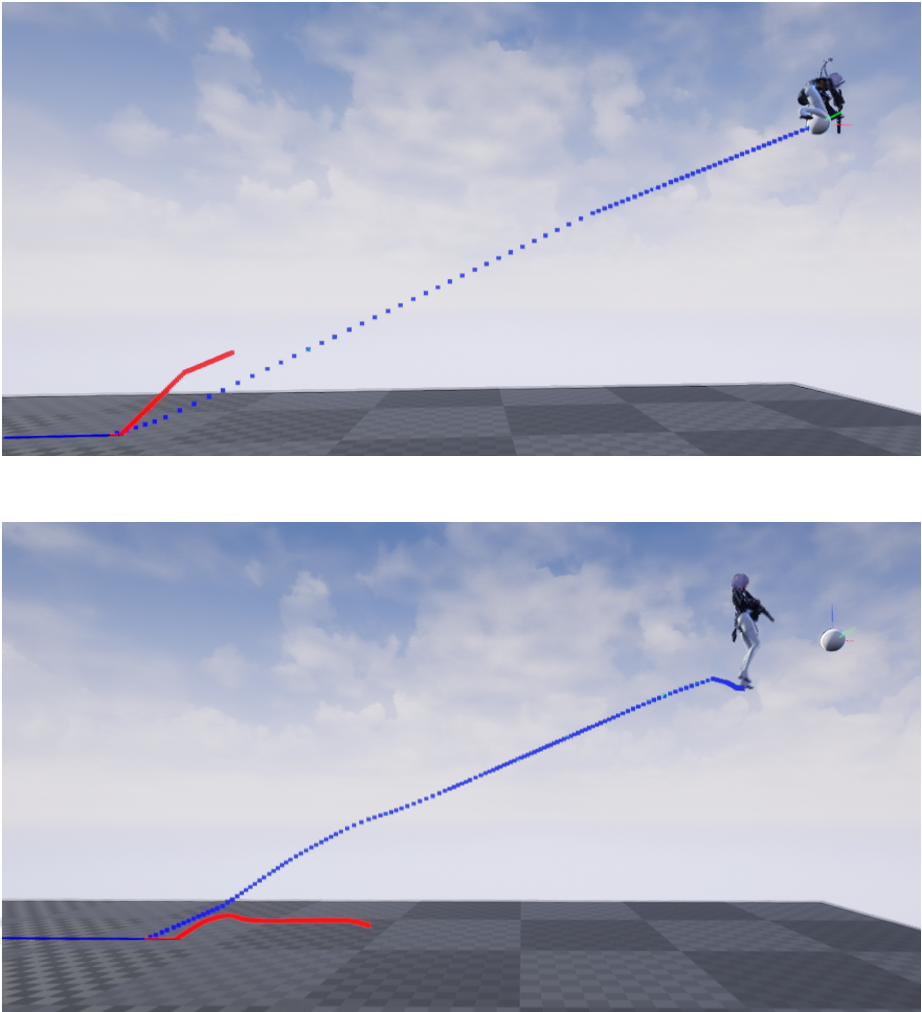SkewWarp能避免突变问题（上图）和多峰值的曲线能更接近目标点（下图）
其他
另外还有Adjustment Blend Warp通过叠加动画的方式应用到腿部骨骼减少Warp造成的滑步问题。带步伐的RootMotion动画使用SkewWarp会有滑步问题，需要自己处理Warping算出来的IK数据。
对于动作游戏，保持良好手感需要支持频繁输入打断。而转身打断只通过旋转胶囊体和融合过渡动画表现不佳
RootMotion Turn + MotionWarping + TimeWarping保证随时能打断，并且平均角速度一致MotionWarp对手感的优化。
参考
Bringing Hell to Life: AI and Full Body Animation in DOOM: https://www.youtube.com/watch?v=3lO1q8mQrrg ↩
Player Traversal Mechanics in the Vast World of Horizon Zero Dawn: https://www.youtube.com/watch?v=LrLHsbTK5bM ↩