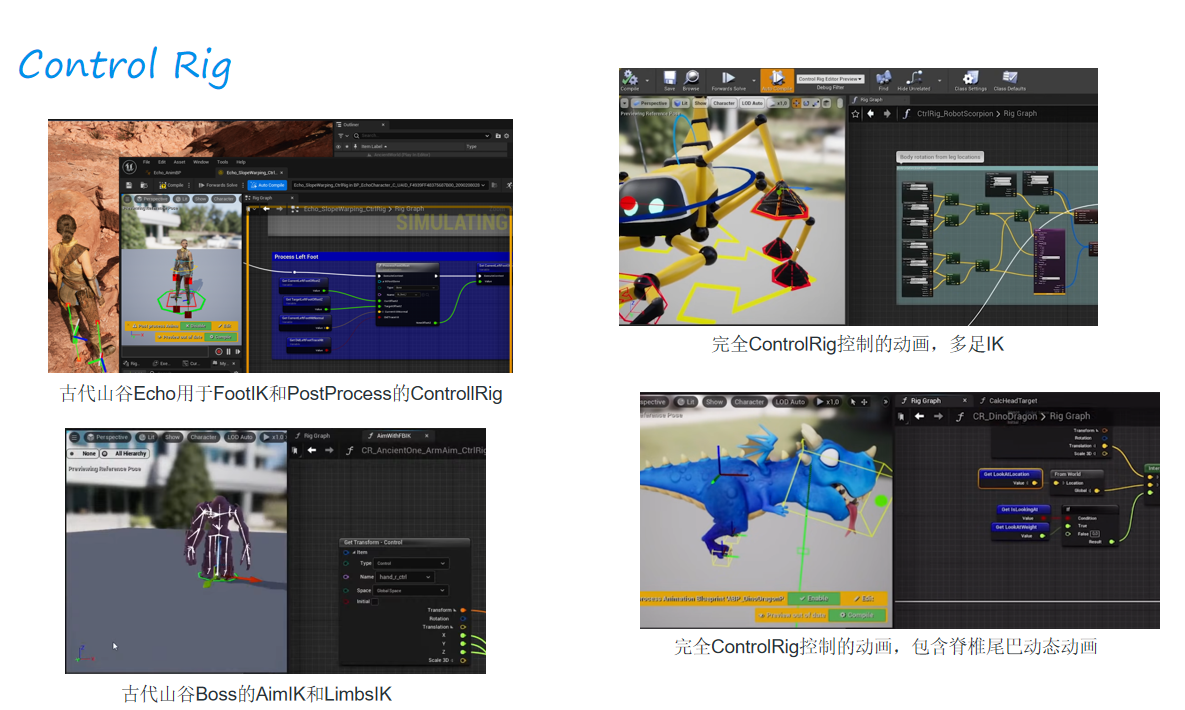
程序化动画

发表于 2023/09/20

作者 lynx 28 分钟阅读

程序化动画是通过算法来生成或修改动画的技术。它不是完全靠手工帧动画，而是用规则、物理模型、生物学特征等“程序”实时或在预处理阶段产生或修正动画表现。它可以“修正变形”——在已有动画基础上自动调整角色姿态或模型形变（比如根据地面高度调整脚的位置）。它可以做“物理模拟运算”——用物理规则让布料、头发、碰撞反应更自然。它还能“延申构造”——基于少量输入生成更多细节（如程序生成的连锁反应、群体行为等）。

程序化动画 != 逆向运动学（IK）。现在有不少教程和文章会把程序化动画等价于动画IK，IK 可以是程序化动画的一部分。比如脚步贴地通常用 IK 来把脚放在正确位置。但程序化动画范围更大：除了 IK（关节求解），还包含物理仿真、动力学、脚本规则、随机性、感知决策、LOD 级别的细节生成等。因此把程序化动画等同于 IK 是片面的。

程序化动画的优势

节省美术资源，提高资源复用度
- 传统做法：每个动作都由动画师手工制作，耗时且难以覆盖所有场景变化（地形、角色尺寸、装备差异）。
- 程序化好处：用一套基础动画 + 程序逻辑，自动适配不同武器、不同地形、不同角色体型，减少对“全新动画”的需求，从而节省人力和时间。
- 如使用Ragdoll、物理动画等，通过物理模拟一帧Idle动画就可以实现撞击、垂直摆动等角色动画效果。
拟真，提高品质和自然感、细节
- 通过物理或生物学启发的规则，动画能表现更自然的小细节（如人物走路时肩膀轻微晃动、根据速度自动改变步幅、武器后坐力的实时响应）。
- 例如：枪械开火时，枪身轻微位移与角色上半身的反应不是预先做好的每一帧，而是实时按力学计算产生。
- 通过实际的场景数据、物理数据等修正动画，让动画更自然。如起步停步需要根据当前速度修正动画播放，防止滑步。
加强互动（场景互动、角色间互动）
- 程序化允许角色在面对动态环境时作出即时响应：被推到墙边会扶墙、被击中会根据力度和方向产生不同反应、多人碰撞时产生连锁影响。
- 这类响应难以靠预录动画覆盖所有情况，程序化能处理高组合数的互动。
- 也是拟真之一，目的是大大提高游戏表现性。通过IK等技术方案，让角色的腿跑在凹凸不平的地面，让角色侧身躲避穿过人群，让角色开门，各种让场景跟人物能进行细节交互。
直接影响 Gameplay（甚至成为核心）
- 有些游戏把程序化机制作为玩法核心：例如利用物理/动画系统产生有趣的 emergent behavior（涌现行为），使游戏体验更丰富和不可预测，从而增加趣味性和重玩价值。
- 动画影响动作游戏手感，四足动画、龙的摆尾动画直接影响到关卡设计。还有一种游戏：生物进化拟真游戏，生物的进化产生的动画直接影响到游戏的核心玩法。

《雨世界》的程序化动画，不同生物动画不同

《gang breast》程序化动画，操控程序化动画就是玩法

IK Rig

育碧在GDC2016分享过他们的IK Rig技术，展示了他们程序化动画的成果：

IK Rig: Procedural Pose Animation by Alexander Bereznyak

传统 Rig：需要手工绑定大量骨骼（主动骨、扭转骨、小骨骼、次级骨骼、碰撞/枢轴、道具挂点等）。
IK Rig：只绑定关键主动骨（头、腰、手、脚等），把扭转骨、小骨骼和次级约束交由引擎通过解算器和约束自动生成和驱动，从而大幅减少手工工作并提高复用性。只需绑定关键骨骼，引擎通过 IK/解算器自动生成次级约束与骨骼行为——同一套 IK 规则可适用于不同体型（通过绑定关键点并让引擎重新计算约束）——可以在引擎内动态改变约束参数（例如手抓持位置、武器偏移），无需重新绑定/导出。

IR Rig解决传统crouch高度不适配

IK Rig实现程序化避障

9个角色；男人和女人；9种角色高度大小；9个做了动画的prop；跟节奏同步；可以蹲下可以攀爬

UE5的Control Rig，也是以实现IK Rig为目标：

IK Solver

IK是近几年来十分热门的研究方向，IK的解算方案很多，下面这几个是UE自带的几种解算器：

Analytic Solutions
- Basic IK: Two Bones IK
Heuristic Solutions
- CCD IK
- Basic FABRIK
Numerical Solutions
- Jacobian Transpose
- Jacobian Pseudo-inverse Damped Least Squares(PIDLS)
Position Based Dynamics

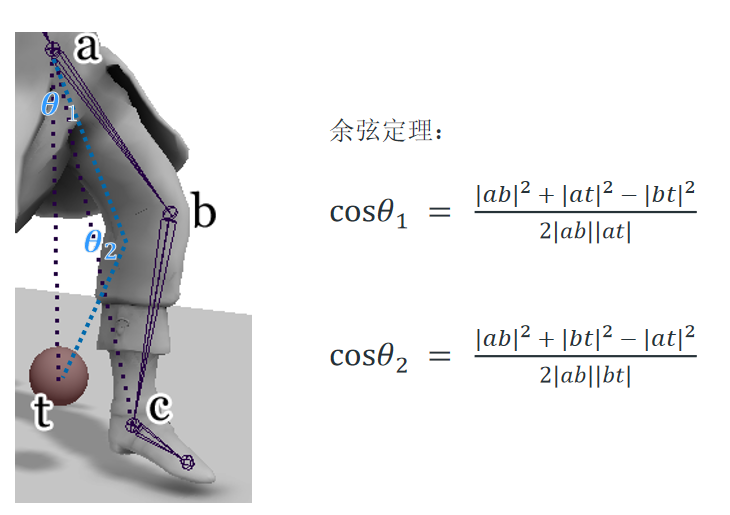
Basic IK / Two Bones IK

这是最基础好算的IK。在只有两根骨骼，三个关节的情况下因为骨骼长是不变的，本质是已知三条边长求角度。余弦定理可得SITA1和SITA2然后根据对应的平面进行旋转。详细可见[推导]。

FABRIK(Forward And Backward Reaching Inverse Kinematics)

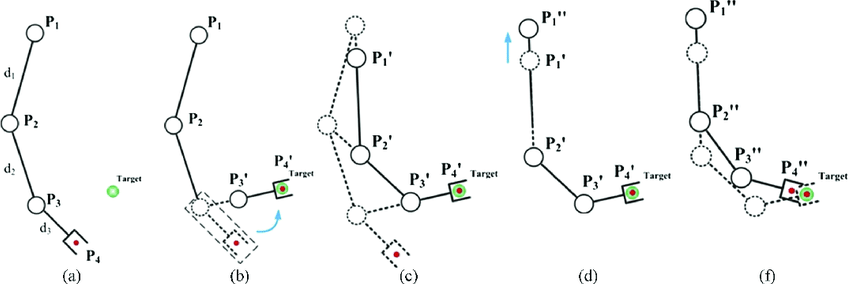
FABRIK（Forward And Backward Reaching Inverse Kinematics，前后到达逆向运动学）是IK解算方法之一。假设有一条由若干关节 P1, P2, P3, P4（根到末端）组成的链，每段骨骼长度固定为 d1, d2, d3。目标是把末端 P4 移到某个目标位置 Target，同时保持每段长度不变（或近似不变）。

FABRIK 的思想：通过两次传递迭代——“向后传递”（从末端朝根）和“向前传递”（从根朝末端），每次按距离约束重新定位关节，通过反复拉扯直至末端与目标足够接近或达到迭代上限。算法过程如下：

图 a（初始状态）

展示初始关节位置 P1..P4 和长度 d1..d3。Target 在末端附近但不重合。
根节点 P1 通常是固定不动（例如角色骨架的根）。

图 b（第一次向后传递开始）

- 第一步把末端 P4 直接移动到 Target：令 P4' = Target。
- 然后从倒数第二个关节 P3 开始：计算 P3' 为位于 P4' 与原 P3 连线方向上并与 P4' 保持距离 d3 的点。
  - 公式（向量形式）： P3' = P4' + ( (P3 - P4') / |P3 - P4'| ) * d3
- 接着以此类推计算 P2'： P2' = P3' + ( (P2 - P3') / |P2 - P3'| ) * d2
- 注意：如果 P1 是固定的，向后传递到 P2' 后要停止（不移动 P1），但 P2' 不再保证与 P1 的距离等于 d1（将在向前传递里修正）。

图 c（向后传递完成，链向根压缩）

显示了所有向后调整后的中间位置（虚线表示旧位置）。末端已对齐 Target，但根到末端链整体可能“缩短”或“偏移”到不满足根固定条件的状态。

图 d（第一次向前传递开始）

- 由于根 P1 固定不动，向前传递从 P1 出发。
- 计算 P2'': 在 P1 到 P2' 的方向上，放置 P2''，使得 |P1 - P2''| = d1：
  - P2'' = P1 + ( (P2' - P1) / |P2' - P1| ) * d1
- 然后计算 P3'': P3'' = P2'' + ( (P3' - P2'') / |P3' - P2''| ) * d2
- 最后 P4'': P4'' = P3'' + ( (P4' - P3'') / |P4' - P3''| ) * d3
- 此时末端 P4'' 可能不再精确位于 Target，形成新的偏差。

图 e/f（向前传递结果，末端偏离）

展示向前传递后链的新位置（P1 固定，末端偏离 Target）。因此需要再次向后传递以收敛。
重复向后/向前传递若干次后，链条在满足各段长度约束下逐步收敛，使末端尽可能接近 Target（若目标在可达距离内则可达到精确到阈值）。
虚线/实线交替表示多次迭代过程中的位移轨迹。

详细可截[FABRIK: a fast, iterative solver for the inverse kinematics problem]

CCDIK(Cyclic Coordinate Descent)

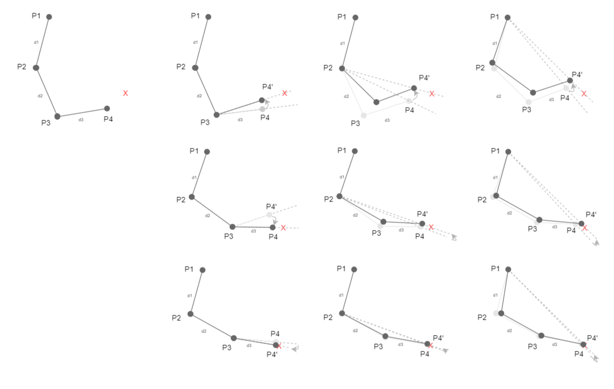
CCDIK（Cyclic Coordinate Descent，循环坐标下降法）也是快速IK解算器之一。通过从链的末端向根部依次逐关节旋转，每次把当前关节转到能让末端更接近目标的方向，循环多次直到收敛或达到迭代上限。

算法步骤如下：

初始（左上）：P1..P4 是一条关节链，末端 P4 离目标 X 有一定距离。
第一步（调整靠近末端的父关节）：固定 P1、P2、P3（临时），以 P3 为旋转中心，计算把 P4 朝 X 方向旋转的角度并施加旋转，得到新的 P4（记为 P4’）。图中 P4 从灰色虚线位置移动到新的实线位置。
第二步（向上一个关节移动）：接着以 P2 为中心，旋转 P2（从而带动 P3、P4）使末端更接近 X，得到新的位置（P4’‘）。
第三步（再向上）：以 P1 为中心旋转 P1，使链更靠近 X。
完成一轮后如果末端仍未足够接近目标，重复从靠近末端的关节开始（即再次从 P3 开始），循环直到误差小于阈值或达到最大迭代次数。
图里的多格展示了多次这样的局部旋转，末端点逐步逼近目标轨迹。

两个快速IK解算器对比：

CCD：逐关节旋转，局部迭代，容易实现，适合实时，但可能收敛慢或陷入局部最优。
FABRIK：直接移动点位置并保持长度约束（前后传递），数值更稳定且通常收敛快，不直接计算旋转角度。

Jacobian IK

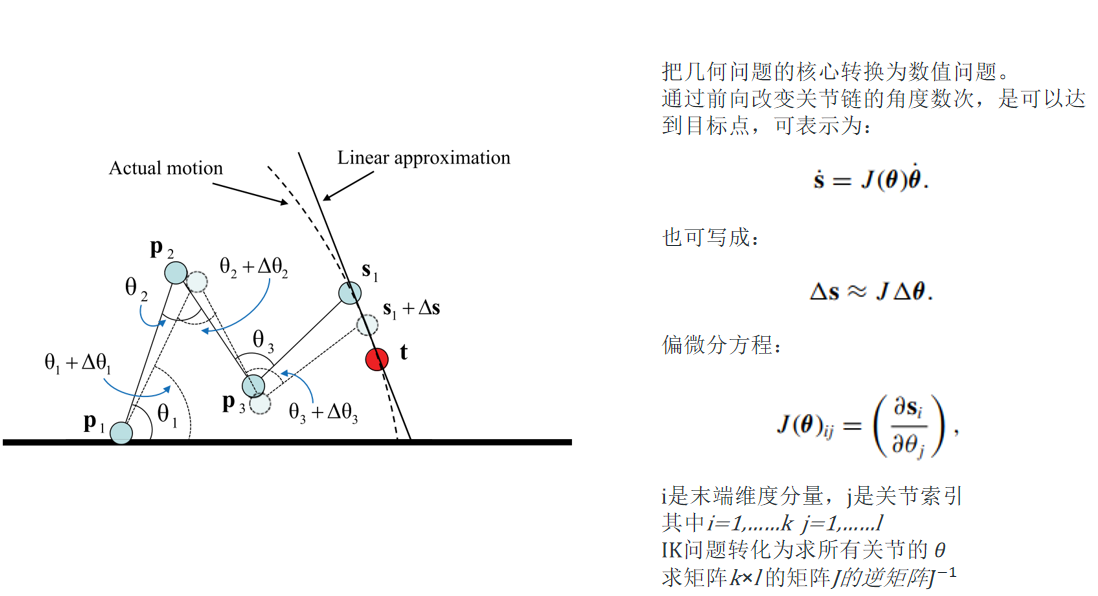
雅可比IK是一个数值法的IK解算办法，它适合多骨骼多目标点的解算的FullbodyIK。核心算法为已知期望的末端位置（或位置变化）s（或 Δs），求一组关节角度 θ（或变化 Δθ），使得机器人臂/角色的末端达到目标位置。末端位置是关节角度的非线性函数$ s = f(θ)$，直接求解$f^{-1}$一般很难（尤其是多关节、约束或冗余情况下）。因此常用局部线性化方法把问题转化为数值问题来迭代求解。

图中显示一条由多个关节组成的链（关节位置 p1, p2, p3…；对应关节角度 θ1, θ2, θ3…）。s1 表示末端在某参考状态下的位置，s1 + Δs 表示经过小幅角度变化后末端的新位置；红点 t 是目标位置（target）。θi + Δθi 表示对第 i 个关节做了小的角度改动；图中用虚线和箭头表示实际运动与用线性近似得到的运动方向的差别（非线性 vs 线性近似）。

速度形式： $ṡ = J(θ) θ̇$ 说明：末端速度$ ṡ$（向量）等于雅可比矩阵 $J(θ)$ 乘以关节角速度 $θ̇$。
位置增量的线性近似（用于小位移迭代）： $Δs ≈ J(θ) Δθ$ 说明：当 $Δθ$ 很小时，末端位置的变化$ Δs$ 可以用雅可比乘以 $Δθ$ 来近似。这个线性近似是牛顿法一类迭代求解的基础。

$J(θ)$ 的元素定义为$J(θ)_{ij} = ∂s_i / ∂θ_j$，也就是末端位置第 i 个分量对第 j 个关节角度的偏导数（局部敏感度）。如果末端空间维度是 m（例如在平面上 m=2，在三维空间 m=3），关节数为 n，那么 J 的尺寸是 m × n。例如三维中末端位置 (x,y,z) 且有 6 个自由度关节，J 为 3×6。每个 ∂s/∂θ 可以通过解析求导（若有 s = f(θ) 的公式，比如链式法则得到位置关于角度的偏导），或者数值差分（把 θj 增加一个小量看末端位置变化）来估算。

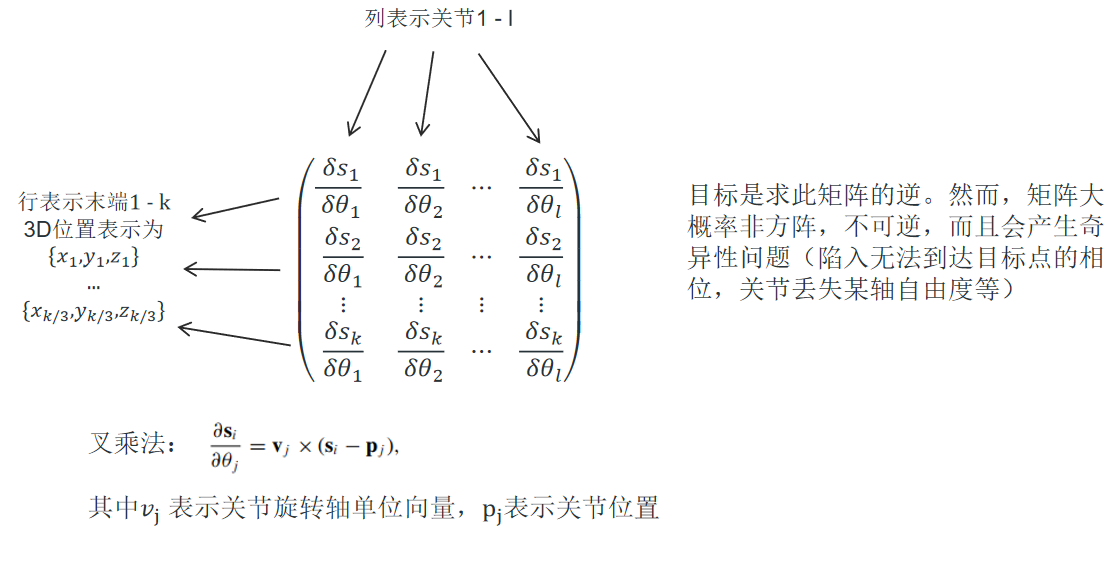
上图为雅可比矩阵的结构形状：

行：末端自由度的分量数 k（例如末端在 3D 空间的位置有 k=3，对应 x,y,z）。
列：关节数量$ l（θ1..θl）$。
因此 J 是 k × l 的矩阵，元素为 $J_{i j} = ∂s_i / ∂θ_j$。

途中给出的常用计算公式是偏导数用叉乘表示的形式： $∂s_i / ∂θ_j = v_j × (s_i − p_j)$ 其中：

$s_i$：末端第 i 个坐标分量对应的位置向量（通常用末端位置向量 s）；
$p_j$：第 j 个关节的位置向量（旋转中心）；
$v_j$：第 j 个关节的旋转轴单位向量（表示旋转方向）；在 3D 中 $v_j$ 是轴向单位向量；
$×$ 表示向量叉乘（cross product）。
含义直观：
- 当关节 j 绕轴$ v_j$ 发生微小角度 $dθ_j$ 旋转时，末端 s 会在垂直于$ v_j$ 的方向上移动。移动向量的方向由$ v_j × (s − p_j)$ 给出（这是末端相对于关节的径向方向在绕轴旋转时的切向方向）。
- 规模方面，末端线速度大体与旋转角速度成比例，且成比例系数与末端相对关节的距离成正比（更远的点移动更大）。

雅可比矩阵工程上常见问题：

奇异性（rank 缺失）：
- J 可能在某些姿态下失去秩（导致伪逆数值不稳定或解不存在），例如手臂伸直导致某些方向失去自由度。
- 处理办法：SVD 奇异值截断、Tikhonov 正则化（damped least squares）、切换到不同 IK 算法（FABRIK/CCD）或添加约束/惩罚项。
单位/坐标系一致性：
- $v_j、$$p_j$、$s$ 都必须在同一坐标系（世界或骨骼统一坐标）下计算，避免因坐标不一致导致错误结果。
数值稳定性：
- 当 r 很小（末端几乎就在关节附近）或$ v_j$ 与$ r$ 几乎共线时，叉乘向量会接近零向量，注意防止除零或施加很大角度更新。
加权/优先级：
- 对不同末端分量（例如位置 vs 方向）或不同目标可以设置权重，在最小二乘求解中体现优先级。

用雅可比求解 Δθ简短流程如下：

在当前 θ 下计算 J（每列按叉乘公式或数值差分）。
计算误差$ Δs = target − current_end_position$。
求解线性问题 $J Δθ ≈ Δs$：
- 若 m × n 情况不同，使用 Moore–Penrose 伪逆 $Δθ = J^{+} Δs$；
- 或使用阻尼最小二乘（Damped Least Squares）： $Δθ = (J^T J + λ^2 I)^{-1} J^T Δs$，这在接近奇异时更稳定（λ 为阻尼项）。
更新关节角度 $θ ← θ + Δθ$（可乘以步长因子 α 以防发散），重复直到收敛。

所以雅可比矩阵的关键还是求J的逆矩阵。关于UE的FullIK，我通过解读源码已知UE5的求逆方法：

Jacobian 转置法（Jacobian transpose）优点计算量小（只需 J^T e，无需矩阵求逆或 SVD），实现简单，常用于实时性强而自由度不太高的场景。缺点是收敛性差（尤其在冗余或接近奇异的姿态），可能需要很多迭代；对尺度敏感（不同关节影响量级差异会导致步长很难选择）；无法保证最小范数解（可能产生不合理大角度）。伪逆阻尼最小二乘法（PIDLS / Damped Least Squares）稳定性好：对奇异位形鲁棒，避免伪逆在小奇异值时数值发散。收敛速度通常优于转置法（因为本质上是最小二乘问题的正规解）。可以通过 λ 控制解的平滑性与跟踪精度之间的权衡（λ 越大，解越保守、越平滑）。缺点则是计算量大。需要调参（λ 的选择）。λ 太小会接近原伪逆导致不稳定，λ 太大导致解保守、精度下降。

XPBD IK

UE5.0之后取代JacobianIK的FullBodyIK方案。PBD是通过约束求解，对于做过布料和流体的同学比较熟悉。

使用XPBD的三节摆

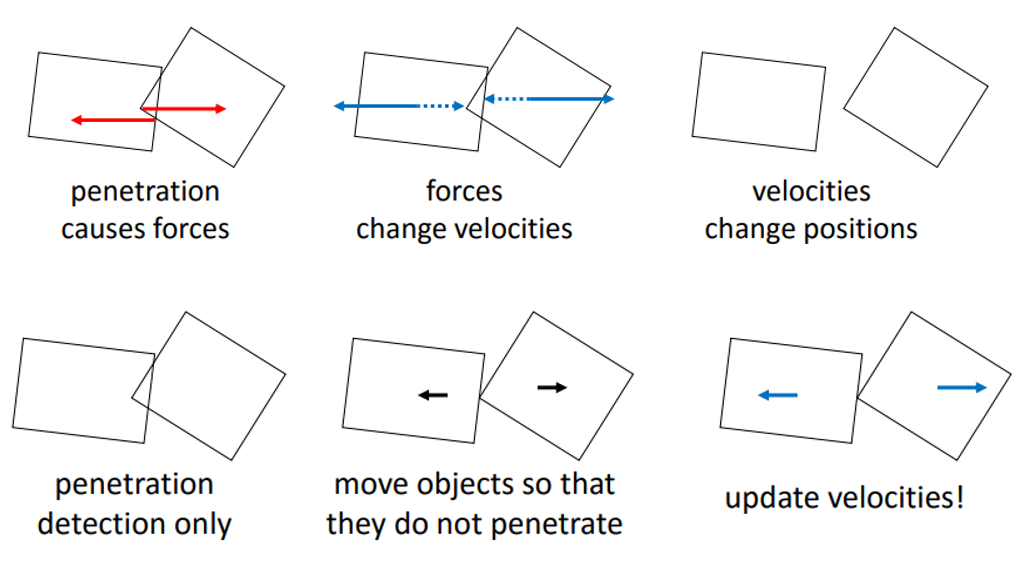
PBD（Position Based Dynamics）核心思想：
- 不是先算力再积分位置，而是先预测位置（基于速度、重力等），然后直接通过“约束求解”修正位置，使之不穿透、满足距离/角度等约束，最后根据位置变化更新速度。
- 优点：数值稳定、易控制、对硬约束（如距离、碰撞）处理直观。
- 基本循环（伪代码图3）：
  1. 预测位置：$x_i ← x_i + Δt * v_i$（并保存上一步位置 p_i）
  2. 对所有约束迭代求解：$compute Δx_i 并 x_i ← x_i + Δx_i$
  3. 更新速度：$v_i ← (x_i - p_i) / Δt$

PBD核心思想图示

PBD 的通用约束形式：
- 对某约束 C，位置修正通常写成 $Δx_i = λ w_i ∇C_i（w_i = 1/mass）$
- PBD 用 $λ = -C / Σ w_i |∇C_i|^2$ （即标准拉格朗日乘子解的简化）
- XPBD 在分母增加了 $α/Δt^2 $项： $λ = -C / (Σ w_i |∇C_i|^2 + α/Δt^2)$
  - 其中 α 是约束“柔度”（compliance）；α→0 趋近于刚约束；α 大时更软。
  - 这个额外项能把约束的响应与时间步长 Δt 解耦（时间步独立性），也能作为阻尼/正则化项，提高稳定性。

XPBD 的工作流程

系统表示：
- 每个骨骼关节 i 视为粒子 i，位置 $x_i$；可能还有旋转变量（旋转可通过位置约束或额外四元数约束处理）。
- 约束集合 C 包含：长度约束（骨骼长度固定）、目标约束（末端靠近目标）、角度/球面锥约束（关节活动范围）、碰撞/不穿透约束、扭转约束等。
每个帧执行（伪代码）：
1. 对所有关节 i：应用外力/驱动（若有）并预测位置 $x_i ← x_i + Δt * v_i$；保存 $p_i ← previous position$（用于更新速度）。
2. 若根固定，强制 $x_root = constant$（或把它作为硬约束）。
3. 对所有约束 C（可以多次迭代，内循环次数 $nIter$）：
```
compute constraint value C(x) // 例如距离误差
compute gradients ∇C_i w.r.t. involved particles
compute denominator = Σ w_i |∇C_i|^2 + α/Δt^2 // XPBD
λ = -C / denominator
for each involved particle i: x_i += λ * w_i * ∇C_i
（可并行或顺序处理不同约束集合）
```
4. 更新速度$ v_i ← (x_i - p_i) / Δt$（可加阻尼/平滑）
5. 将位置$ x_i$ 应用回骨骼变换
约束求解通常需要多次迭代（Gauss-Seidel 式），以便在多个互相约束的条件下收敛。

可能解释得不够，详情可见论文和视频：

https://matthias-research.github.io/pages/publications/posBasedDyn.pdf
https://matthias-research.github.io/pages/publications/PBDBodies.pdf
https://www.youtube.com/watch?v=jrociOAYqxA&ab_channel=TenMinutePhysics

物理动画

未完待续…

物理动画

本文由作者按照 CC BY 4.0 进行授权

程序化动画的优势

IK Rig

IK Solver

Basic IK / Two Bones IK

FABRIK(Forward And Backward Reaching Inverse Kinematics)

CCDIK(Cyclic Coordinate Descent)

Jacobian IK

XPBD IK

物理动画

热门标签